什么是红黑树
红黑树也是一种平衡二叉搜索树,也是一种平衡树,就是不会出现严重“瘸腿”的现象,出现了就会自动触发平衡操作来维持整棵树的平衡!
为了解决二叉搜索树的平衡问题出现了平衡树,而平衡树的两大代表可以说就是AVL树和红黑树,就目前这状况,红黑树更加吃香!
既然有了AVL树为什么还要有红黑树呢?
AVL树的平衡是依据平衡因子,就是左右子树高度差不能大于1,这个规则其实过于严格,带来的结果就是几乎每次的插入删除新节点都会破坏平衡!
红黑树具有如下特点:
- 也是一种二叉查找树,所以具有二叉查找树的特点,也就是比左边的都大,比右边的都小
- 根节点是黑色
- 默认将空节点作为叶子结点,且是黑色
- 红色节点的左右孩子必须是黑色
- 每个节点到达其所有可达叶子节点路径上的黑色节点数量必须一致
- 每个节点要么红色要么黑色
如下图:
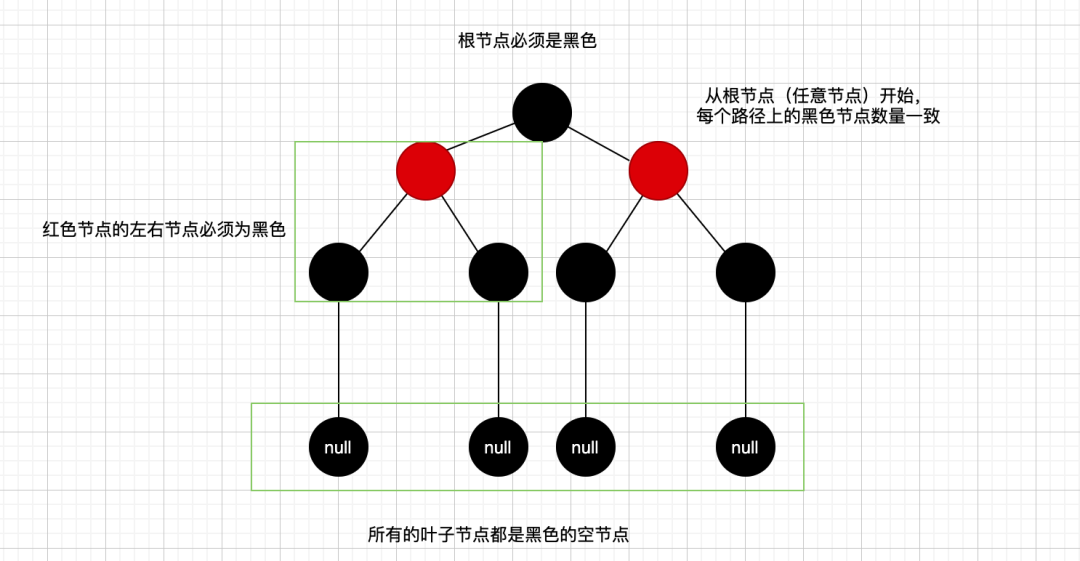
解读红与黑
我们直观的去看红黑树,与AVL最大的区别可能就是红色与黑色了,在红黑树中,用红色和黑色给每个节点着色,通过颜色来维持平衡!
也就是说,在红黑树中,每个节点都有一个颜色属性,也就是每个节点要么是黑色,要么就是红色,而且每个节点的红色黑色也不是随意的,而是有规则的!
红黑树的破坏
红黑树主要就是依据红黑两种颜色作为限制去维持一个平衡,在什么情况下平衡被打破了,我们来看一个例子:
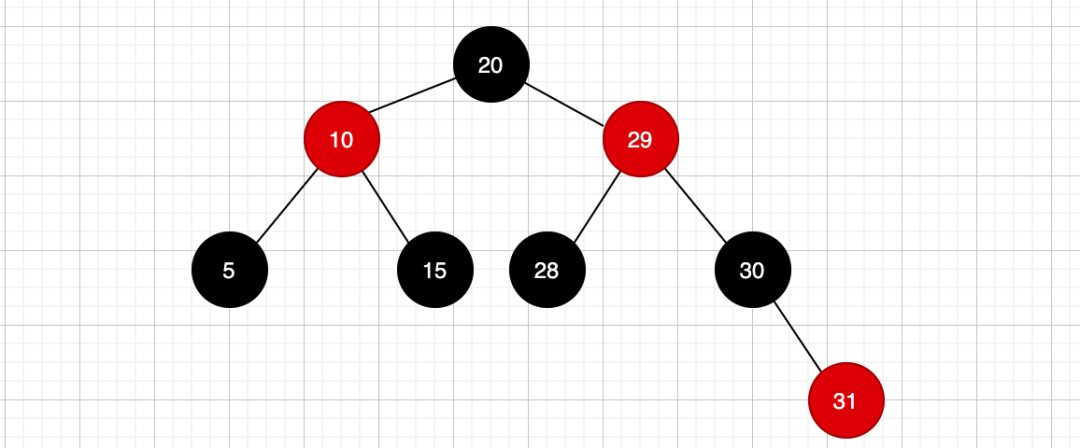
此时还是一颗红黑树,因为现在依然符合红黑树的规则,这个时候就不用做任何调整。但是如果是下面这样:
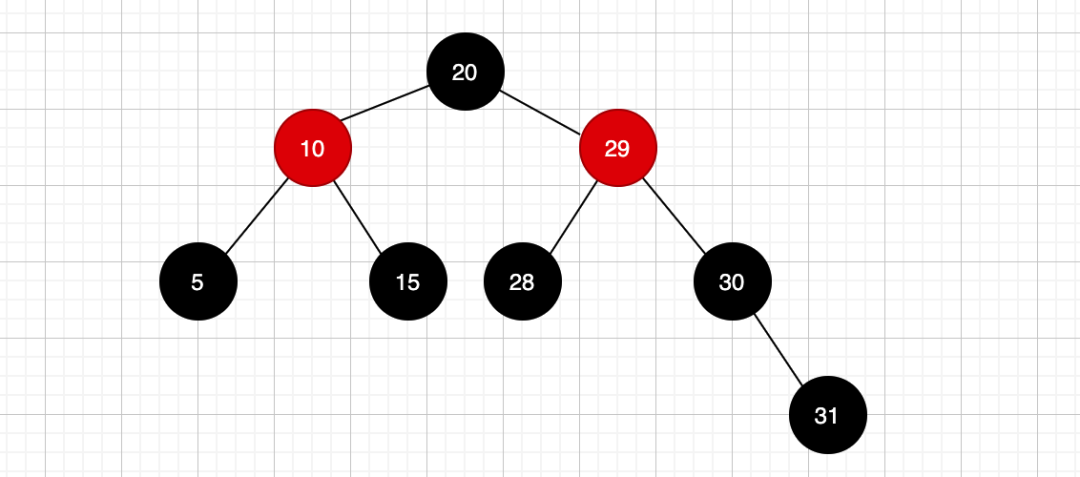
此时就不是红黑树了,为啥?因为它破坏了红黑树的这个规则:
任意节点到该节点可达叶子结点路径上的所有黑色节点数量是一样的
这个时候就得进行调整了,也就是会触发自平衡,通过调整重新让它符合红黑树的规则!
红黑树的平衡
对于红黑树的平衡,有两种方法:
- 通过旋转,也就是和AVL的旋转一样,左旋和右旋
- 通过改变节点的颜色,也就是对节点重新着色
变色处理
我们先来看变色,现在是这样:
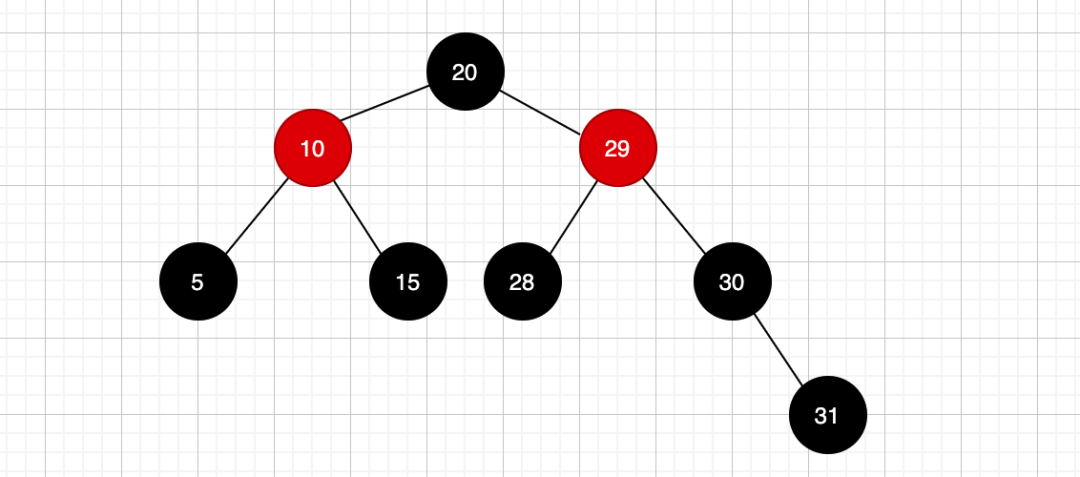
也就是插入了一个黑色节点31导致红黑树失衡了,通过变色也就是对节点重新变色来重新达到红黑树平衡!
插入的31是黑色节点,导致这个路径上的黑色节点多了一个,这个时候就需要把一个黑色节点给变成红色节点!
这个时候我们看,根节点20没法变,必须是黑色,然后29本身就是红色节点,咋搞,只能是黑色节点变成红色了,也就是这样:
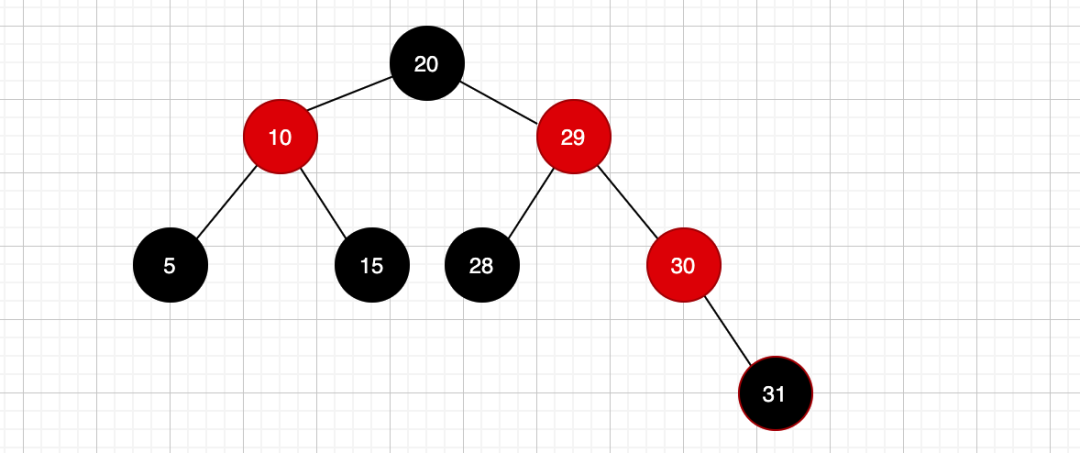
但是这个时候也有问题了,不满足:
一个红色节点的两个孩子必须是黑色
咋搞,只能把节点29变黑了,也就是这样:
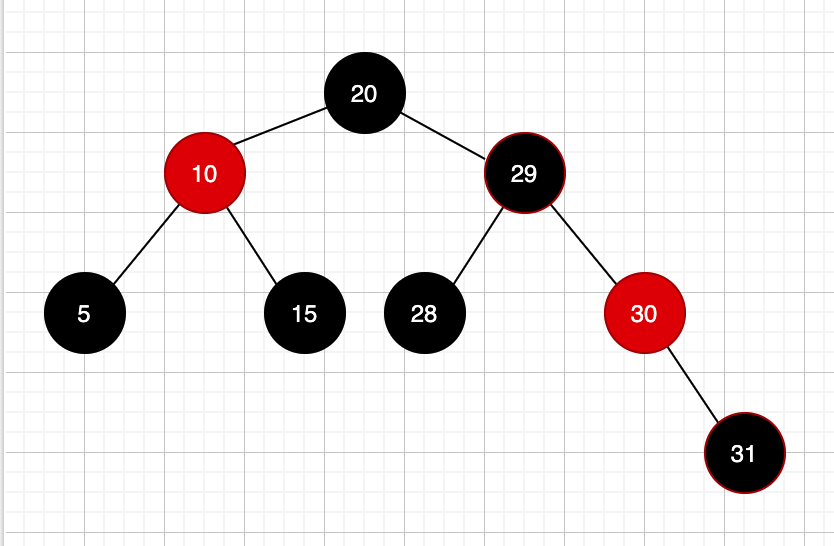
这个时候就要注意看了,此时根节点20的右子树路径上的黑色节点都是一样的,都是3个,此时会发现,左子树上的少一个黑色节点,也就是只需要把节点10变成黑色,整个红黑树就平衡了
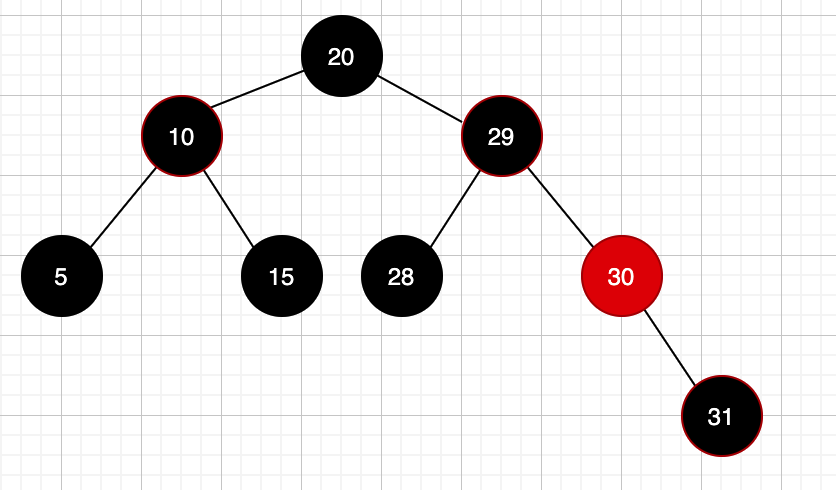
以上就是通过变色的方式去调整使得红黑树再次达到平衡!
旋转处理
接下来我们再来看如何通过旋转来调整红黑树,在说之前,有必要先来了解下旋转的基础操作左旋和右旋,看图:
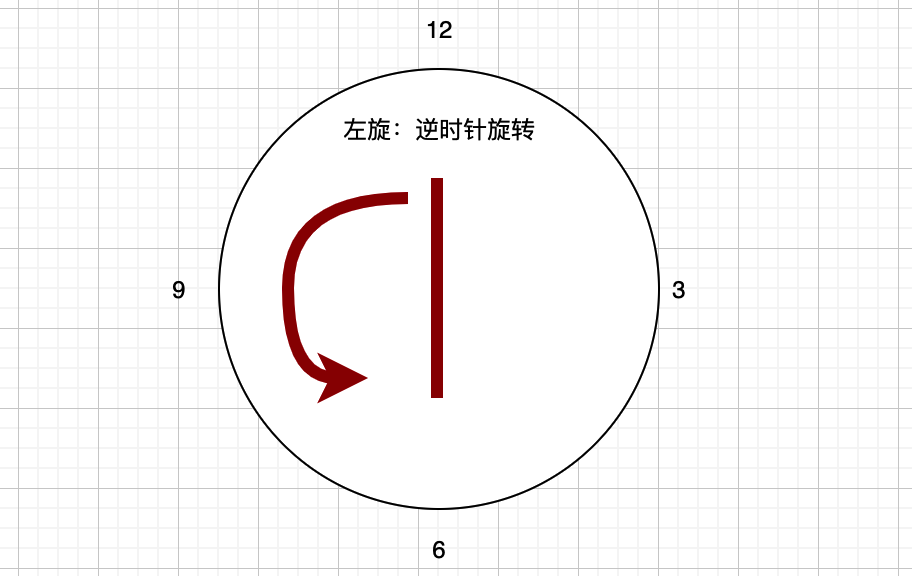
要记住,左旋是逆时针操作,而右旋是顺时针操作,如图:
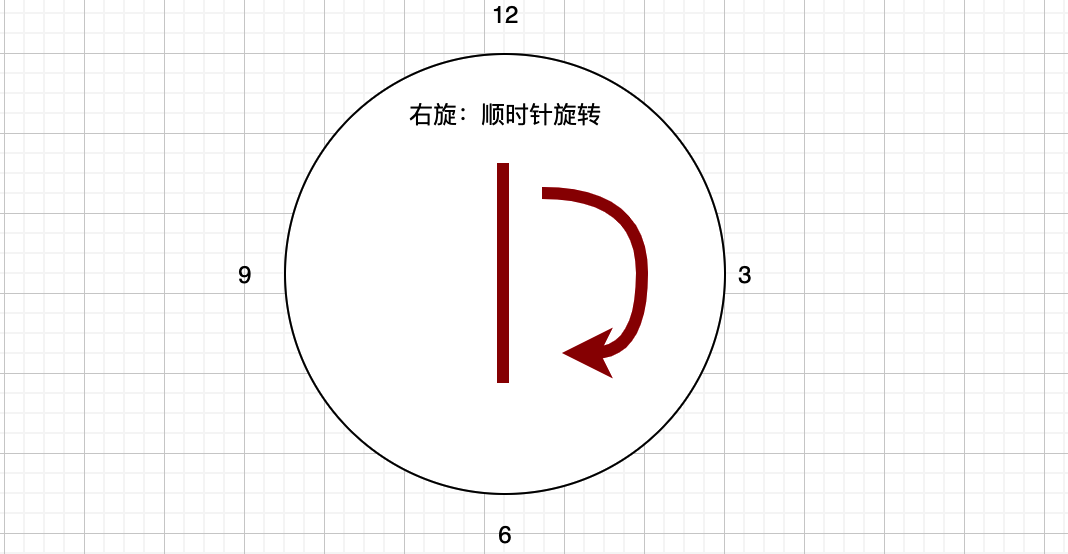
这里有个左右旋的口诀:
左旋:左 - 右 - 左 - 右(把赶走的节点作为该节点的右孩子)
右旋:右 - 左 - 右 - 左(把赶走的节点作为该节点的左孩子)
看个例子:
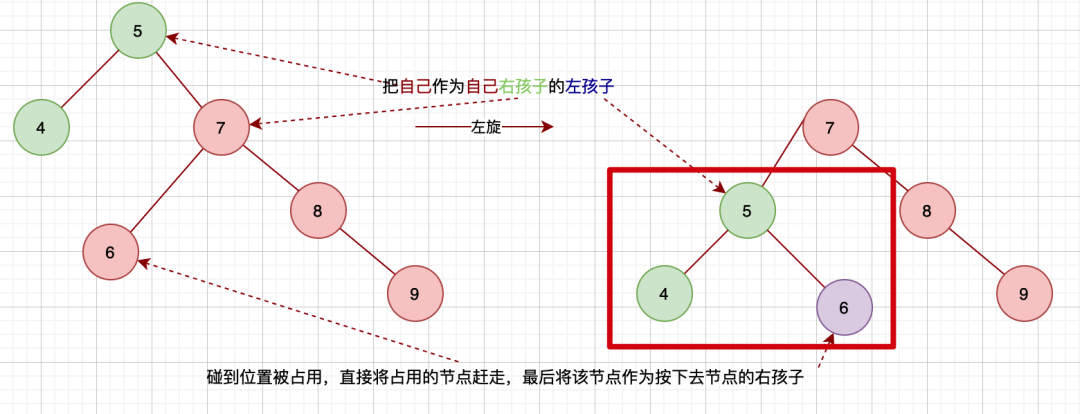
接着我们来看通过旋转的操作使得红黑树达到重新平衡,看下面的一个案例:
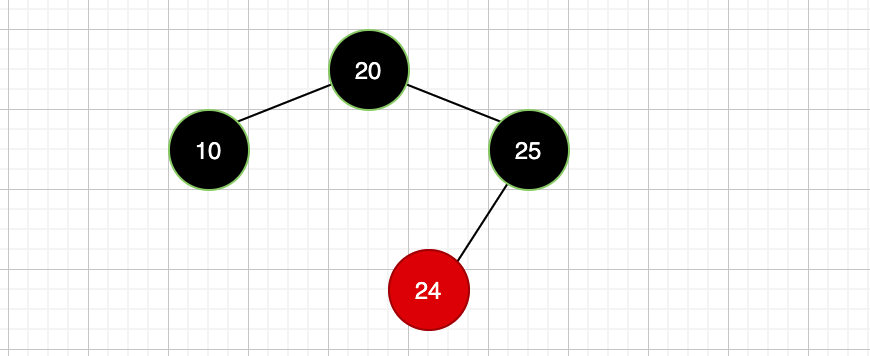
我们看这样的一颗红黑树,此时没啥问题,不过如果我要加入一个新的红色节点21会怎样?是不是就成了这样:
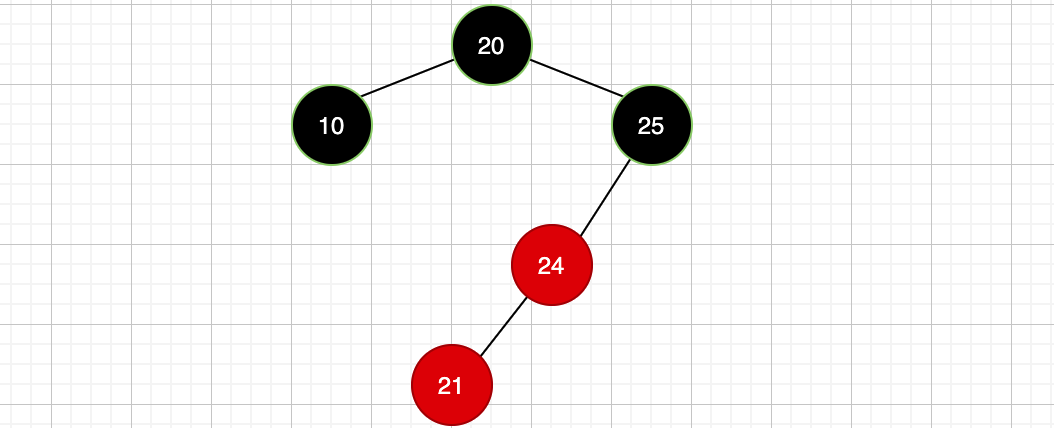
这样红黑树就不平衡了,不满足:
每个红色节点的左右孩子必须是黑色节点
怎么弄?你可能会说变色啊,好,那我们试试变色,此时新插入的节点是红色节点21,变色的话那就是把其父节点24由红色变成黑色,也就是此时这样:
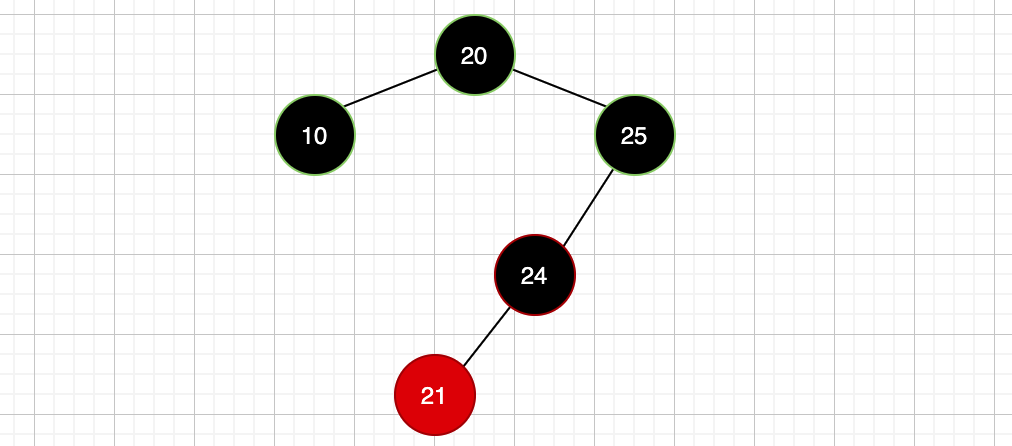
但是现在也出现新问题了,就是每条路径上的黑色节点数量不一致,怎么办?黑色节点25由黑变红?
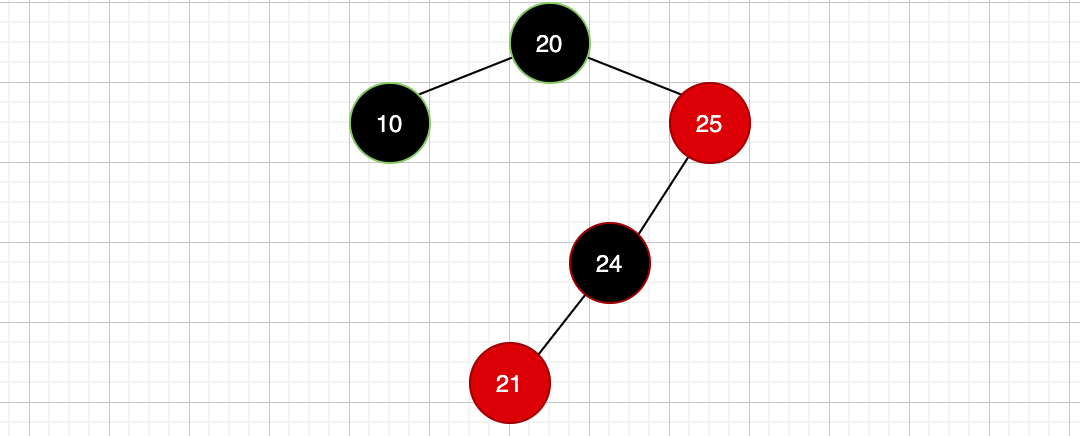
这样可以了吗?答案是不可以,请一定注意看这条规则:
每个节点到达其所有可达叶子节点路径上的黑色节点数量必须一致
有人可能会说,这不是一致的吗,黑色节点不都是两个,大家一定注意了,不是这样的,不知道大家在看红黑树定义的时候有没有疑惑这条规则:
默认将空节点作为叶子结点,且是黑色
据我了解,很多人会把这个规则忽视掉,而一旦把这个规则忽视,你就会对红黑树的一些平衡产生疑问,甚至深陷其中,根据这个规则,我们把上面的情况补充下就是这样的:
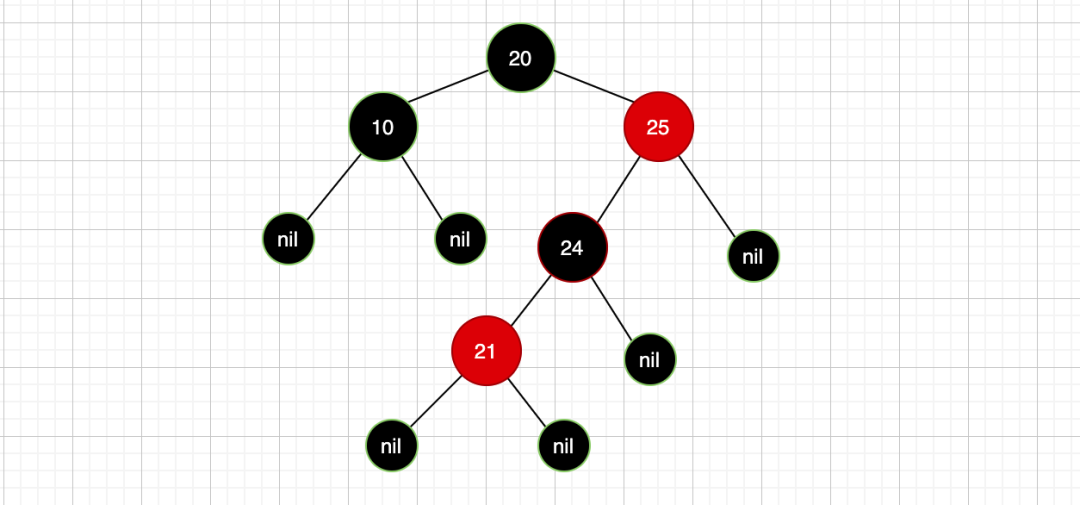
此时红色节点25,它的左右子树路径上的黑色节点可是不一样的
那此时我们再看这个该怎么处理:
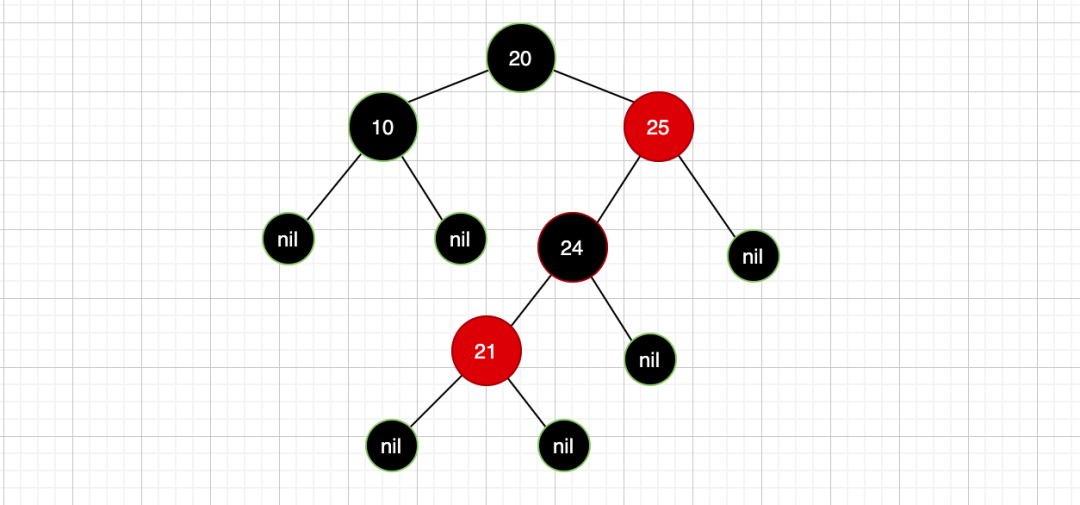
此时节点25红色,但是该节点的左右子树路径上的黑色节点不一致,在往上变色已经没意义了,所以此时要对红色节点25进行旋转操作,怎么选?可以发现它的左子树过深,所以进行右旋:
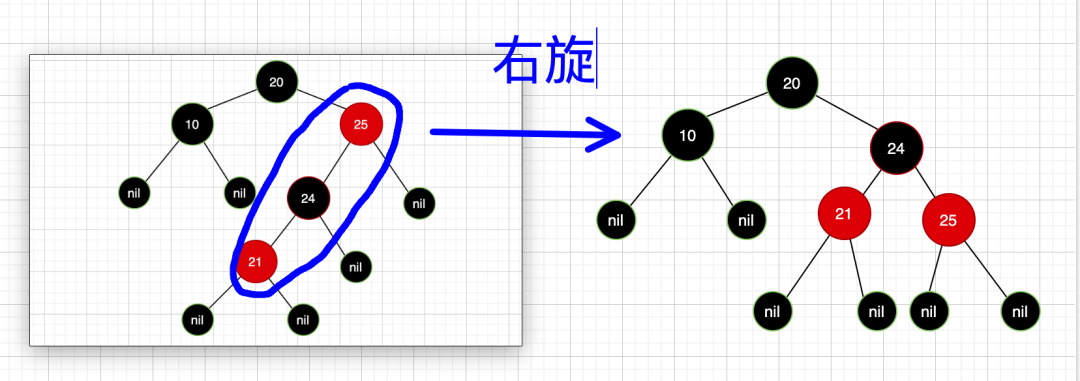
最终也就是成了这个样子:
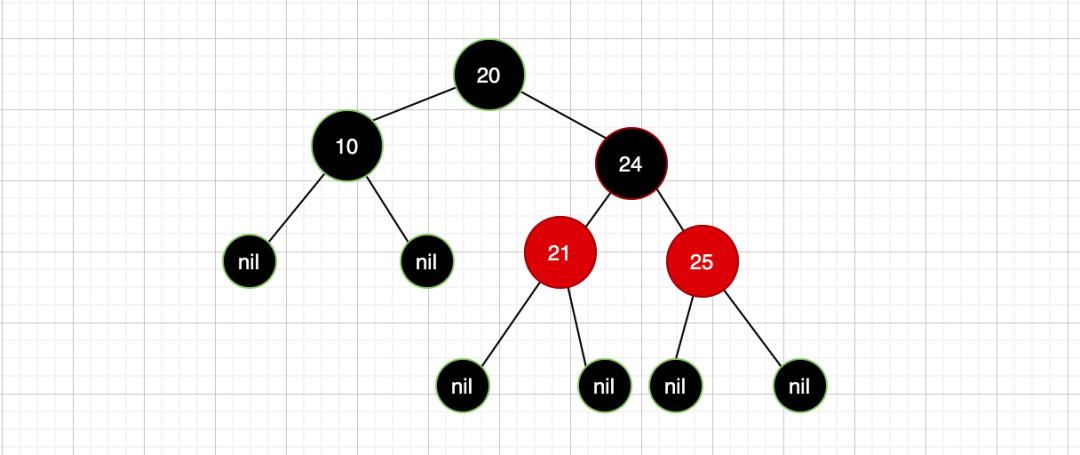
有一条红黑树的规则千万不要忽视:
默认将空节点作为叶子结点,且是黑色
我们一般插入的新节点默认都是红色,为什么?
这是因为更好的适应红黑树的这条规则:
每个节点到达其所有可达叶子节点路径上的黑色节点数量必须一致
试想一下,如果默认插入是黑色,那一定会破坏平衡,每次插入都需要重新平衡,而默认红色就不一定每次都破坏平衡,所以默认都是插入的红色节点!
了解了这个我们继续把注意力拉回到这张图上:
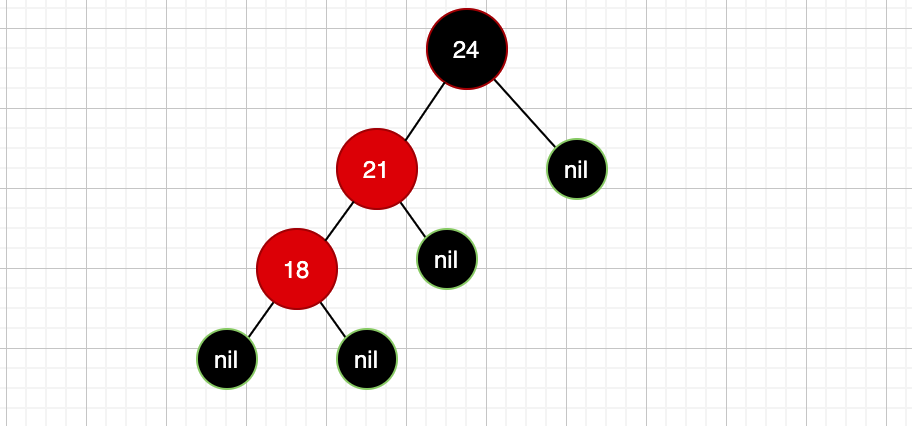
此时我们新插入的红色节点18导致了红黑树失衡,然后我们通过变色,怎么变?记住,向上变,也就是变其父节点的颜色,这里就是把红色节点21变成黑色:
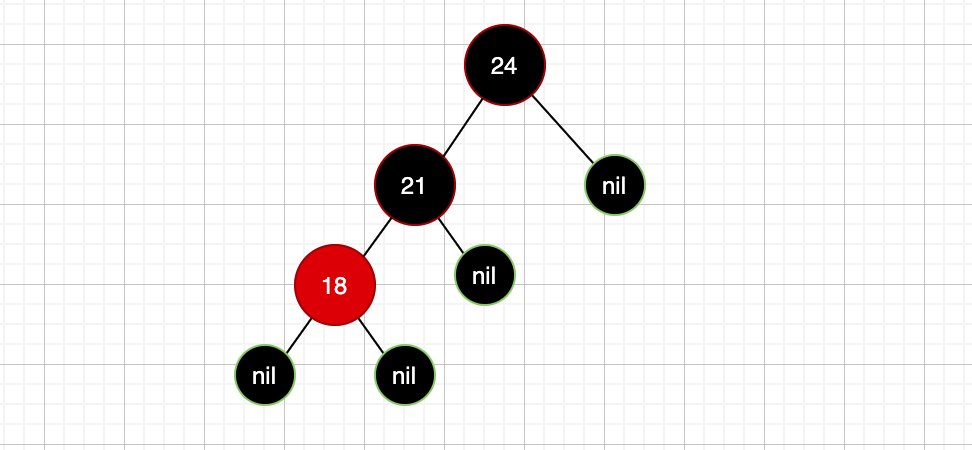
经过变色,现在就成了这样,要记住,此时依然是不平衡的,依然不满足:
每个节点到达其所有可达叶子节点路径上的黑色节点数量必须一致
不满足的点就是根节点24,我们称之为失衡点,那继续变色啊,此时继续向上变色,也即是把根节点24变成红色:
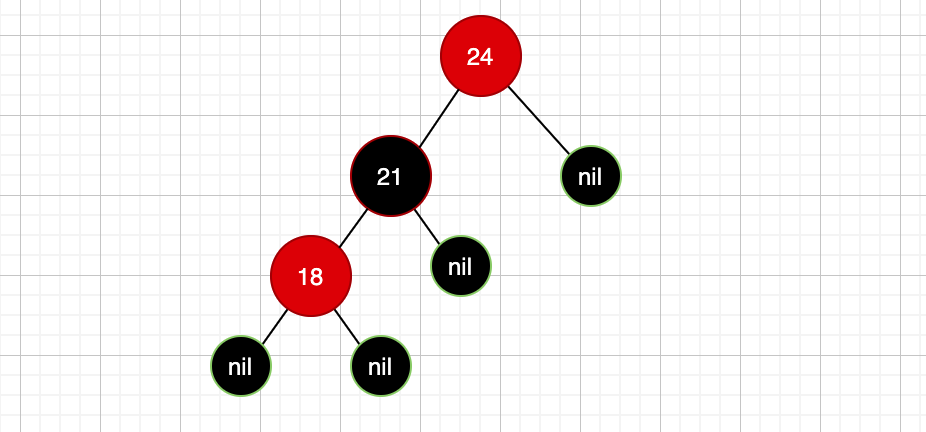
可以看到此时,红黑树依然不平衡,咋整?没节点可以继续变色啦,已经变到根节点了,那此时就要进行旋转了,怎么旋转,左侧深,那就是右旋,就是对根节点24(因为24是一个失衡点,左右路径上黑色节点不一致)进行右旋操作:
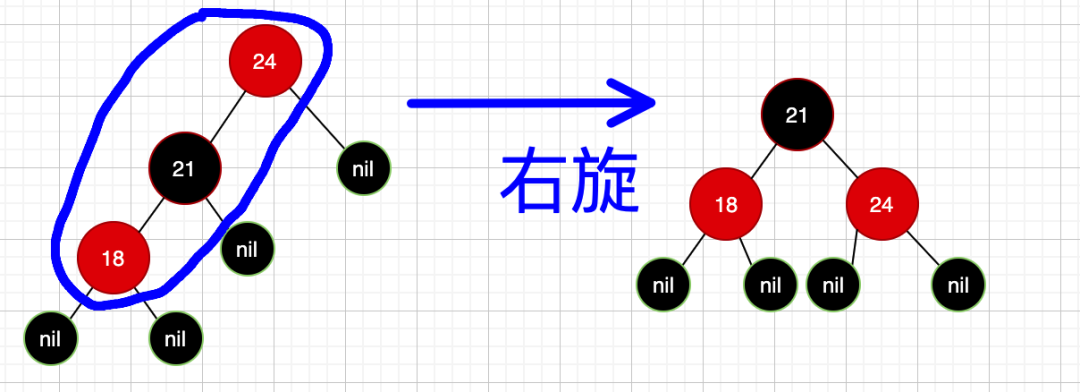
如此一来,红黑树重新达到平衡!
这里有几个关键点要知道:
- 要清楚为什么每次插入的都是红色节点
- 要注意存在空子树的时候是否符合任意节点路径上的黑色节点数量一致
- 可以通过变色和旋转来重新平衡,需要两者结合的时候,先变色或者先旋转都行,只要最后达到平衡即可
红黑树的删除
接下来聊聊红黑树的删除操作,直接看例子:
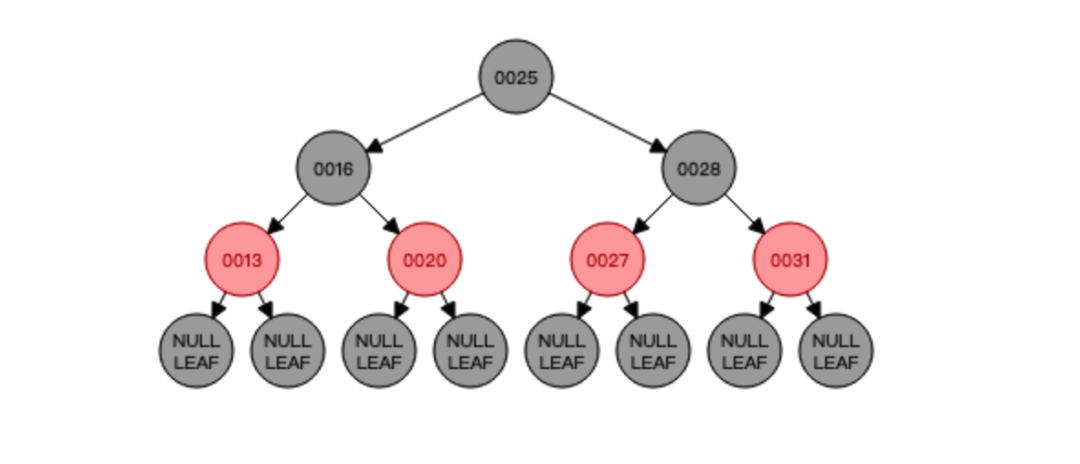
这是一颗正儿八经的红黑树,现在我们删除一个节点,比如删除节点31,成了这样:
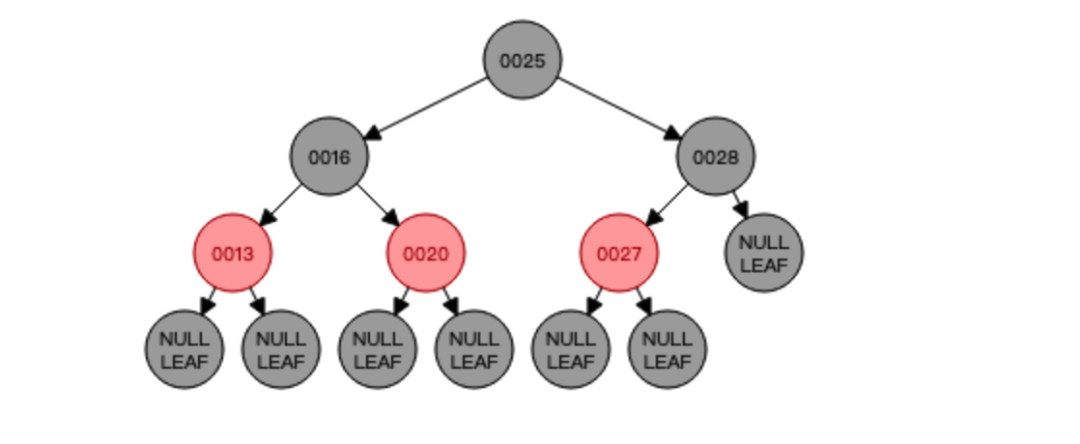
直接删除即可,依然保持平衡,不用做任何操作(红色叶子节点直接删除),但是如果我们删除的是这个节点呢?
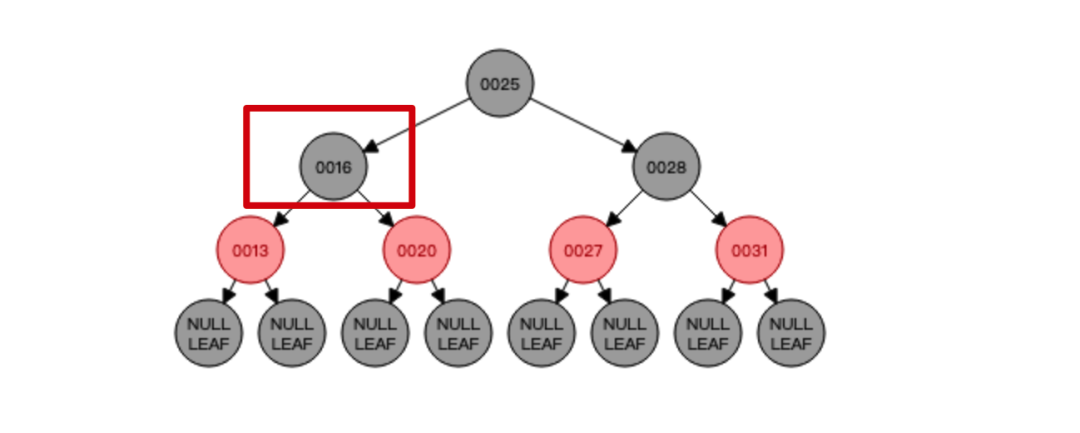
随之而来的问题就是节点13和节点20哪个与根节点25相连?
删除的节点是非叶子节点,则用对应的中序遍历的前继节点顶替要删除节点的位置,删除之后再做重新平衡的操作(如有需要)
然后我们来看该二叉树的中序遍历顺序:
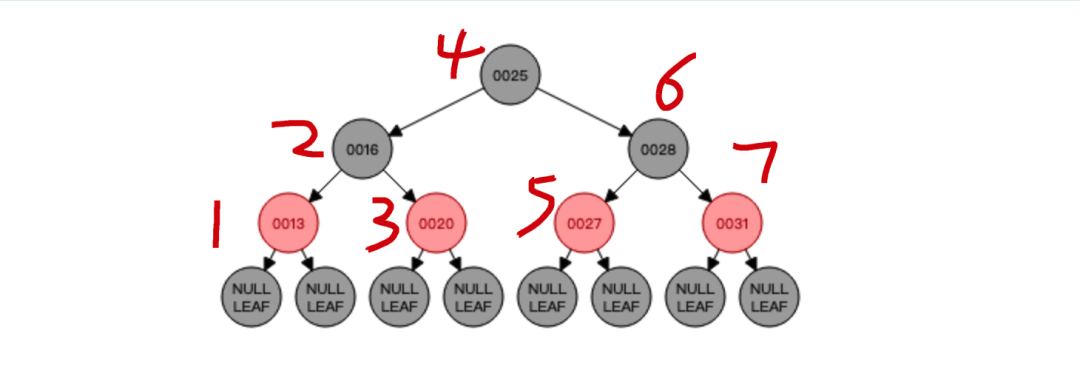
这里中序遍历有个技巧,就是:
按照节点值大小从小到那排序即可
知道了中序遍历的顺序以后,我们就可以进行红黑树的删除了,比如删除节点16,那就需要找到节点16的前驱节点也就是节点13将其替代,也就是这样:
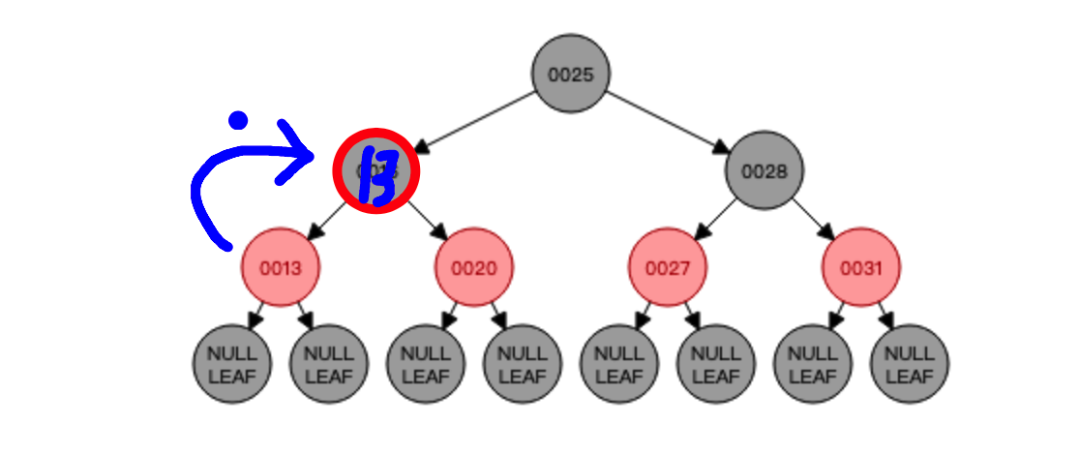
此时原本黑色节点16就被它的前驱节点也即是红色节点13覆盖了,覆盖完以后需要把原来的节点13删掉,也就成了这样:
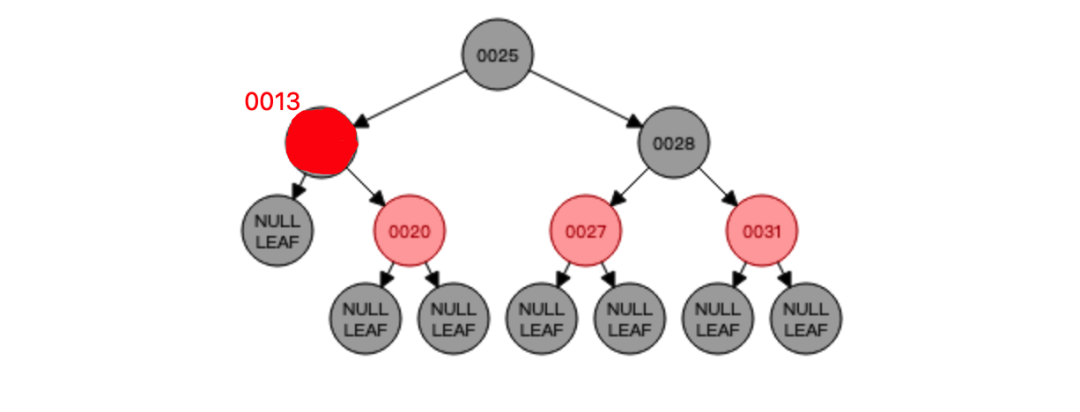
此时发现红黑树不平衡了,就需要进行调整,怎么调整呢?自然是变色,需要把新上位的节点13从原来的红色变成黑色:
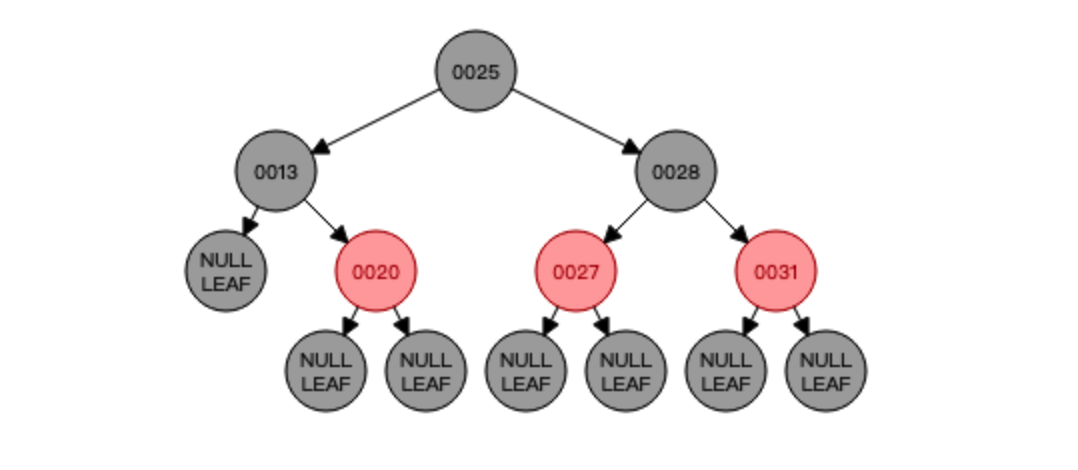
最终这样就达到了平衡,来动图感受一下:
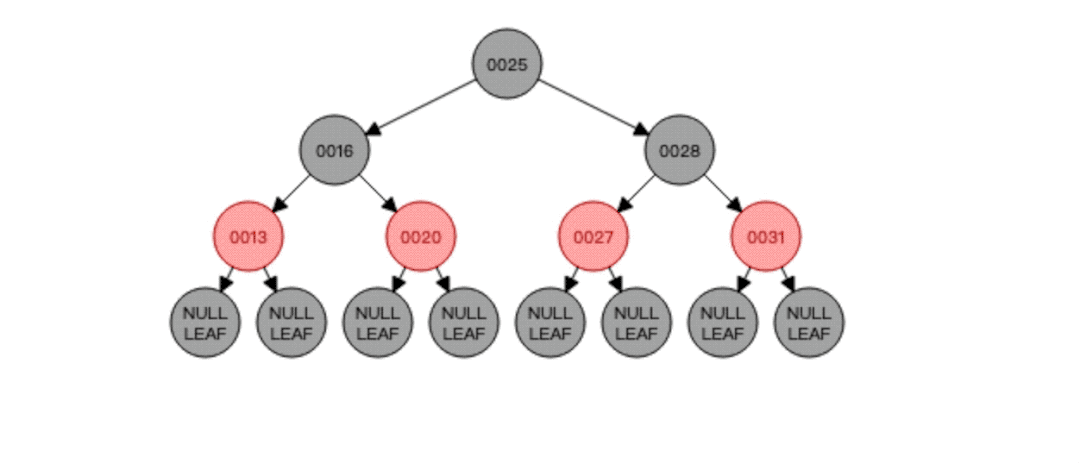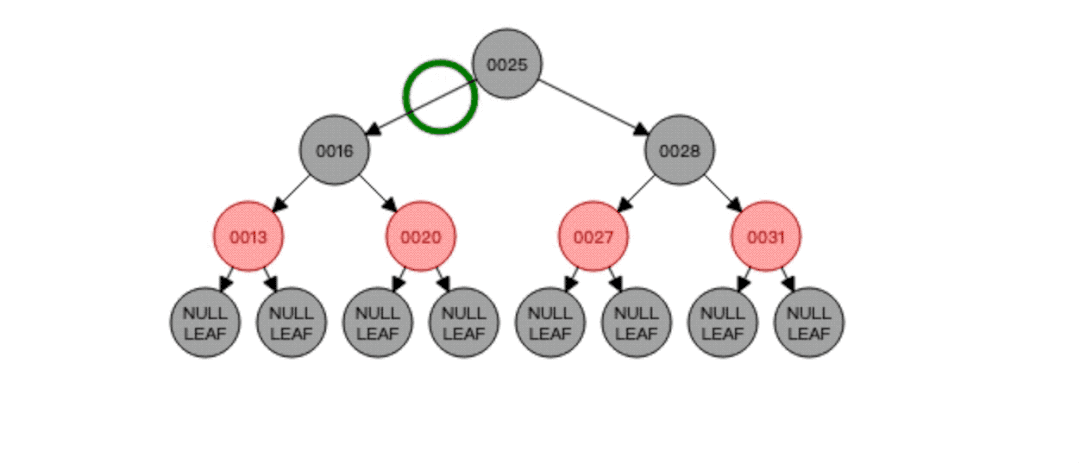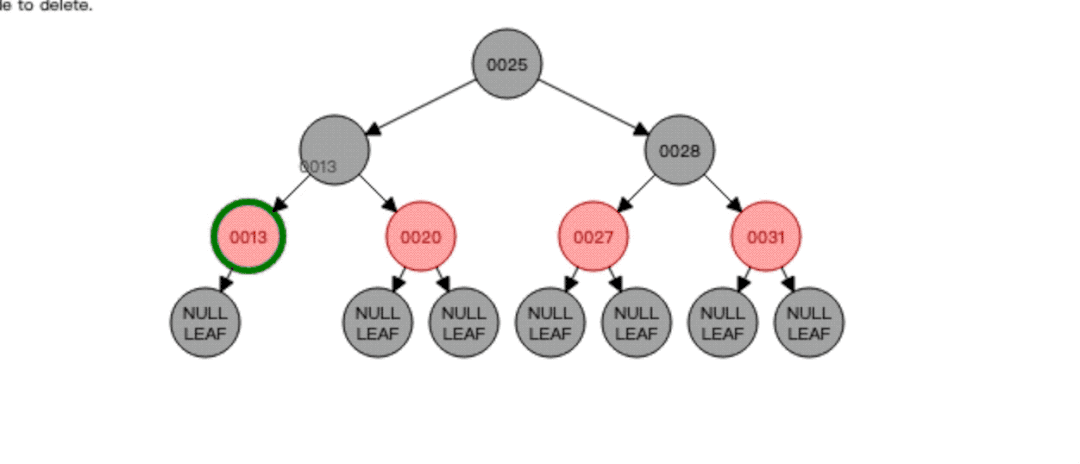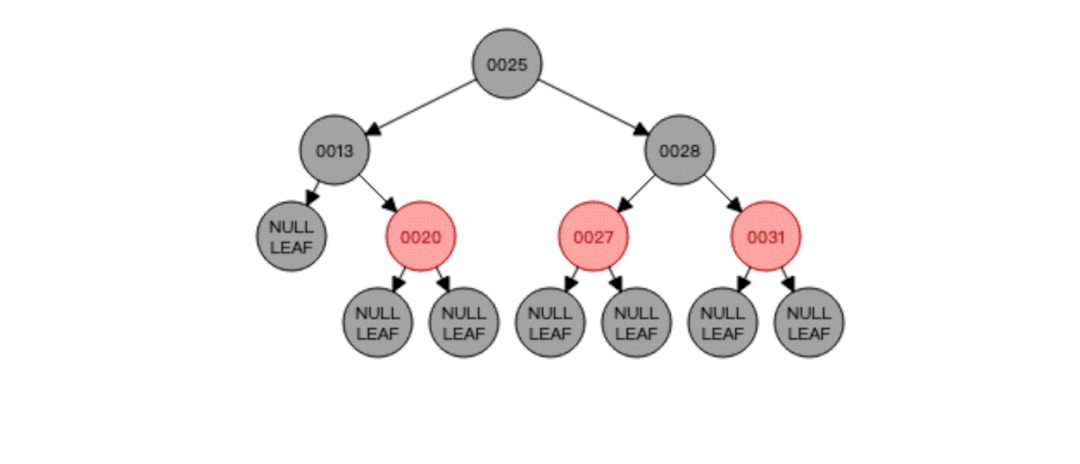
紧接着,我们再看一种情况,还是下面这棵红黑树:
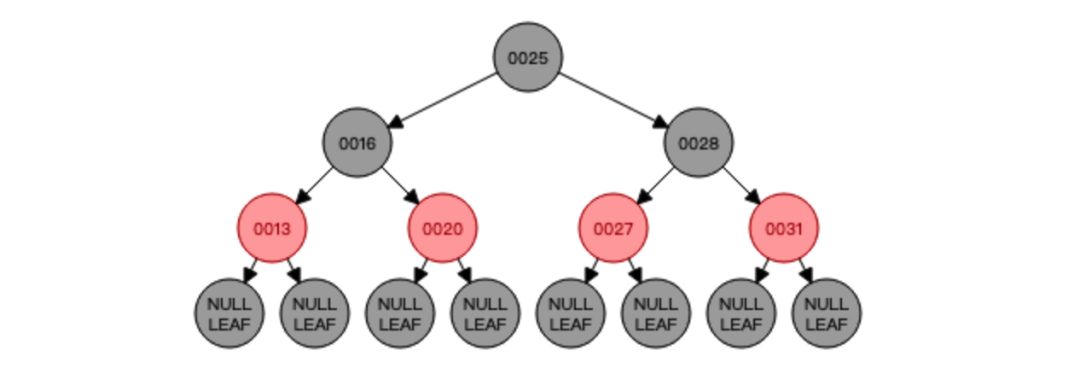
假如现在我要删除根节点25会怎样?直接动图感受一下:
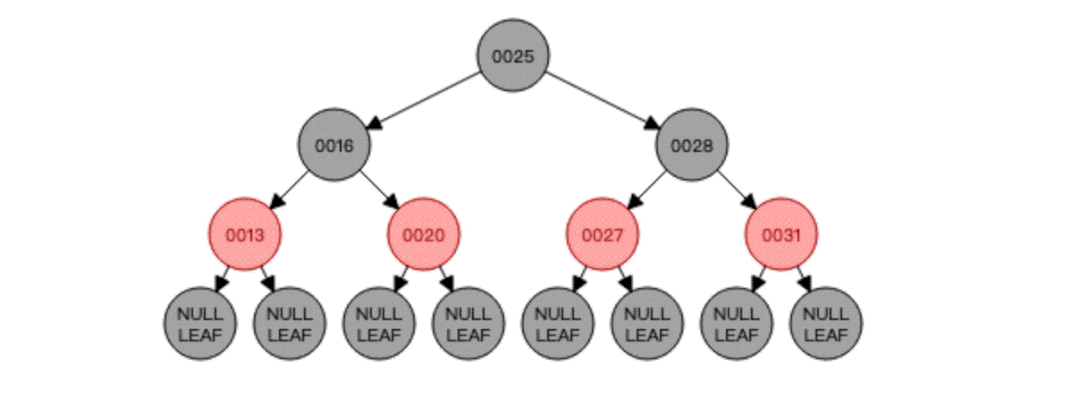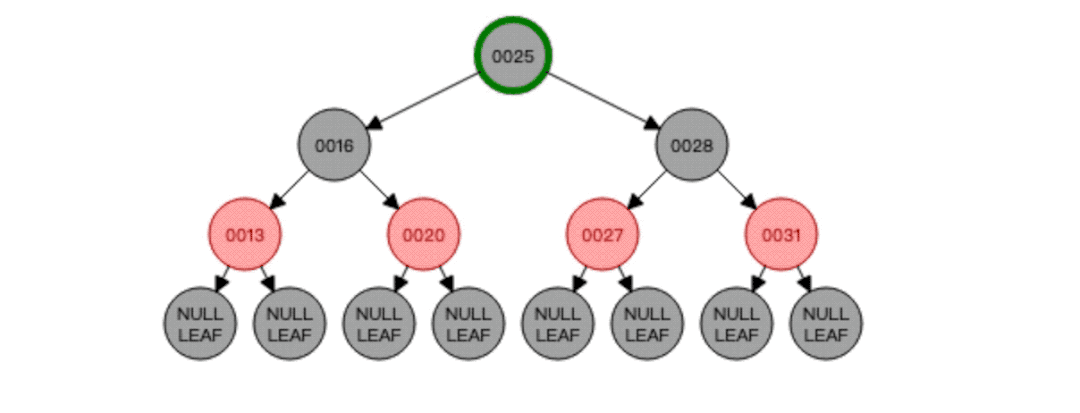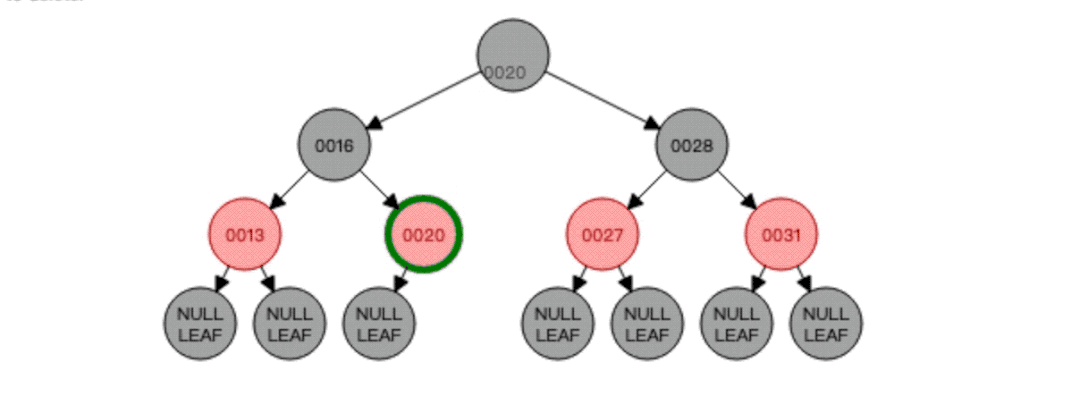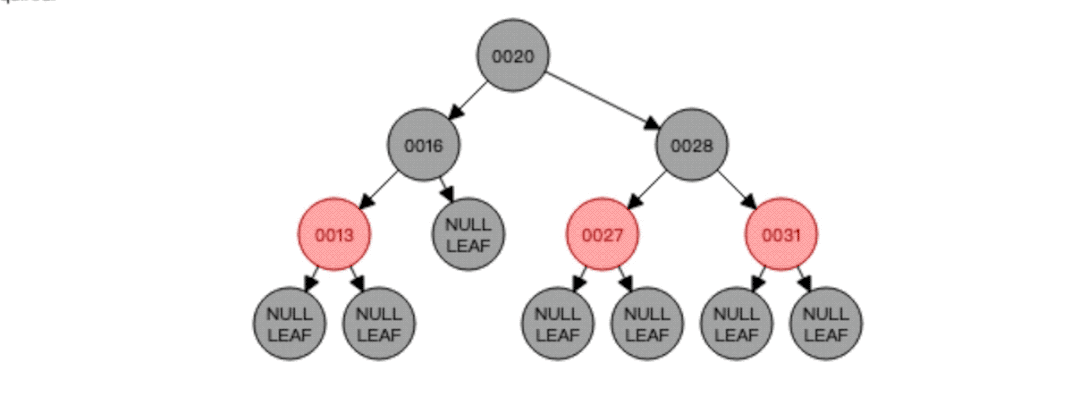
根据动图我们可以发现,先找到要删除的节点25,然后就去找25的前驱节点20,将20复制一份覆盖掉要删除的节点25,然后删除掉节点20,因为节点20是红色,根节点必须黑色,所以覆盖后还需要将节点20调整为黑色,至此红黑树平衡!
对于删除,重要的就是找到要代替删除节点的新节点,删除后如果红黑树平衡遭到破坏就需要进行自平衡以达到红黑树的再次平衡!
关于红黑树的删除操作,公认是比较难且复杂的,对于学习来说,我们需要掌握最基本的红黑树规则,然后知晓一些替换技巧等,剩下的就是依据具体删除的节点去做自平衡操作,也就是删除节点后,需要进行一系列的操作将红黑树再次达到平衡!