1 简单了解下
在了解RSA算法之前,先简单说明下密码学基本原理
1.1 对称加密算法
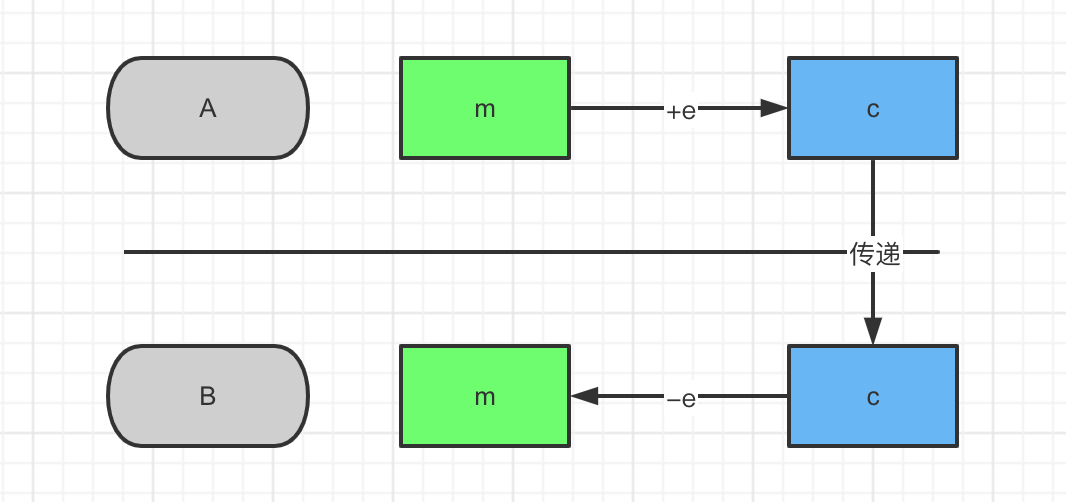
对称加密采用单钥密码系统的加密方法,同一个密钥可以同时用作信息的加密和解密
这种加密方法称为对称加密,也称为单密钥加密
1.1.1 对称加密的缺点
- 密钥如果被窃听,则会被破解
- 可以通过“穷举法”破解
1.2 非对称加密
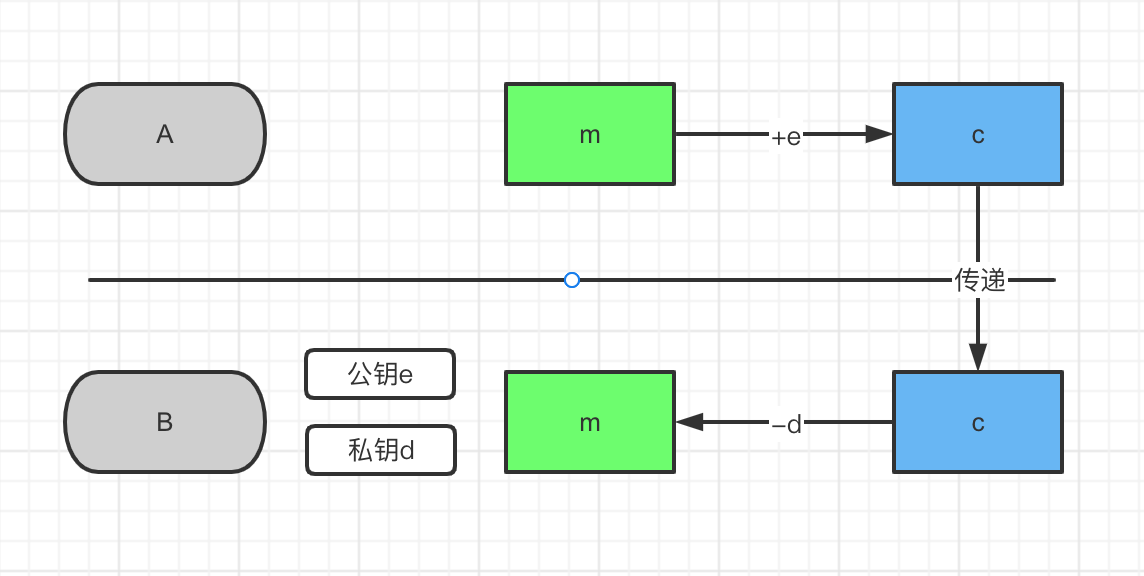
非对称加密算法需要两个密钥来进行加密和解密,这两个密钥是公开密钥(public key)和私有密钥(private key)
1.2.1 非对称加密的缺点
- 大部分情况下,相对于对称加密,效率较低
2 RSA加密算法
最典型的非对称加密算法RSA
RSA公钥加密算法是1977年由Ron Rivest、Adi Shamirh和LenAdleman在MIT(美国麻省理工学院)开发的
2.1 RSA基本原理
// 生成私钥文件
privateKey, err := rsa.GenerateKey(rand.Reader, bits)
- 1.随机取两个质数p,q
- 2.做一个算法n=p*q
n的长度即为密钥长度 - 3.欧拉函数:φ(n)=(p-1)(q-1)
//欧拉函数是小于n的正整数中与n互质的数的数目 totient := new(big.Int).Set(bigOne) - 4.公钥e,1 < e < φ(n) 的整数,且e和φ(n)互质。
两个正整数只有一个公约数1时、它们的关系叫做互质、如3和11互质 - 5.私钥d,e*d除以φ(n)余数为1
//公钥
// A PublicKey represents the public part of an RSA key.
type PublicKey struct {
N *big.Int // modulus
E int // public exponent
}
//私钥
// A PrivateKey represents an RSA key
type PrivateKey struct {
PublicKey // public part.
D *big.Int // private exponent
Primes []*big.Int // prime factors of N, has >= 2 elements.
// Precomputed contains precomputed values that speed up private
// operations, if available.
Precomputed PrecomputedValues
}
2.1.1 进行加密
$m^e$除以φ(n)的求余数 c
2.1.2 进行解密
$c^d$除以φ(n)的求余数 m
3 RSA的安全性
rsa算法的安全性基于大整数质因数分解
思考:有没有可能通过公钥计算出私钥?